和 Vicky 一起学习 Scratch 系列之二十 | 递归算法
前言
上一期,我们学习了一个有趣的数学概念 —— 斐波那契数列,并使用 Scratch 绘制了一条斐波那契螺旋线。
今天,我们将开启算法王国的大门,学习一种很有趣的算法 —— 递归,并使用这个算法创作一个小的作品。
再谈斐波那契数列
上一期中,我们了解了什么是斐波那契数列,这个数列的前几项是这样的:
0, 1, 1, 2, 3, 5, 8, ...
Fibonacci numbers
我们当时还写出了这个数列的公式:
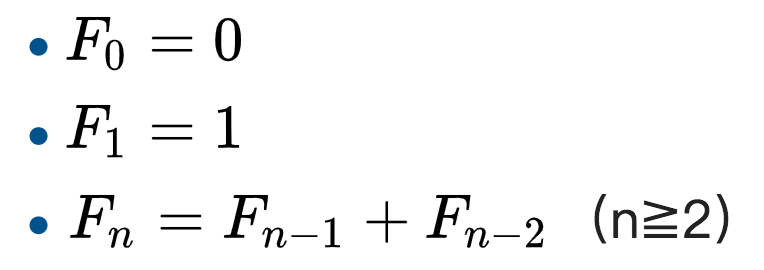
斐波那契数列公式
这个公式怎么理解呢?我们分步解释一下:
- F0 = 0:表示当 n = 0 时,这个数列的值就是 0,这是一个初始值
- F1 = 1:表示当 n = 1 时,这个数列的值就是 1,这也是一个初始值
- Fn = Fn-1 + Fn-2:表示当 n > 1 时,这个数列的值是 前两项的和。
这里的第三行 Fn = Fn-1 + Fn-2 就构成了递归。
递归 Recursion,在数学与计算机科学中,是指在函数的定义中使用函数 自身 的方法
Wikipedia
除了斐波那契数列外,在数学中还有很多递归的例子,其中最为著名的就是 汉诺塔问题 Tower of Hanoi,大家可能都玩过这个游戏:
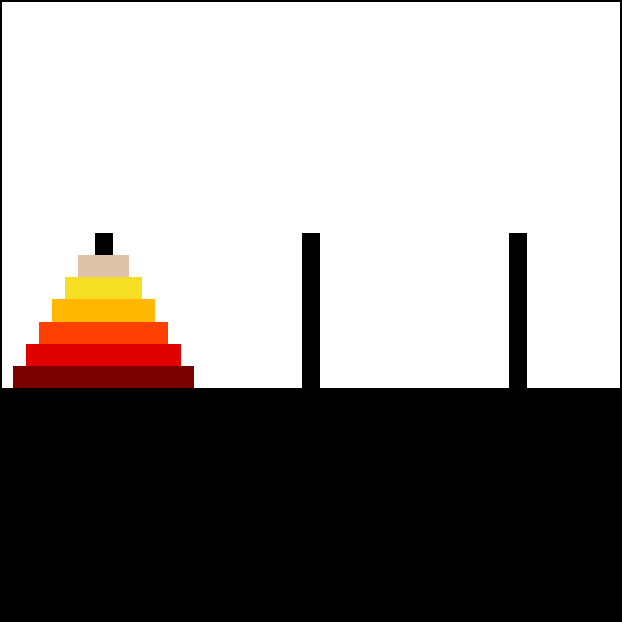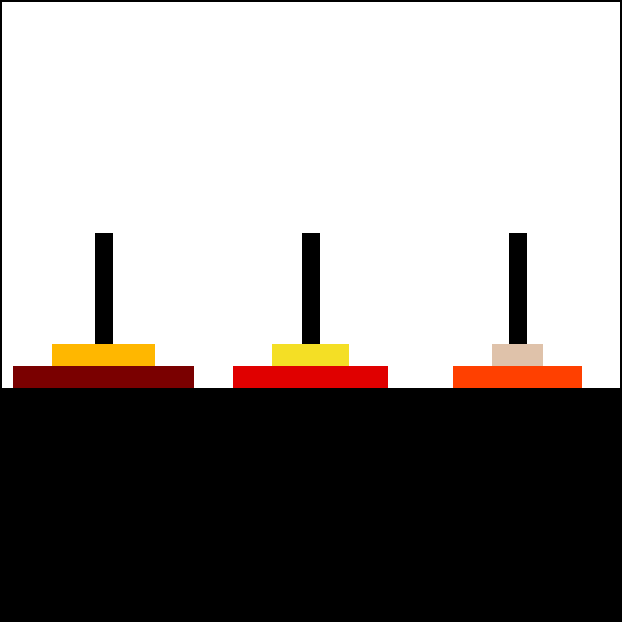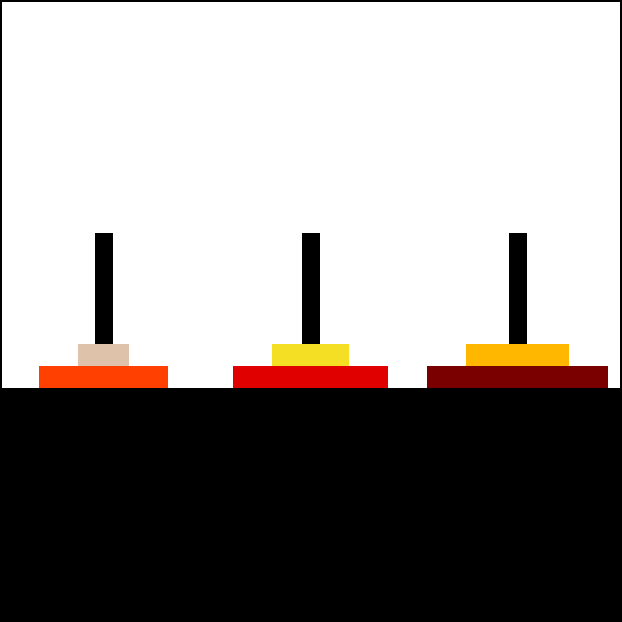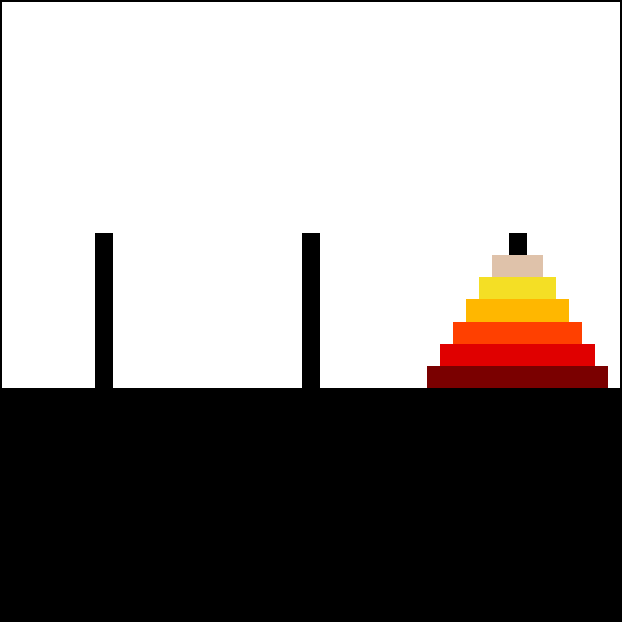
Tower of Hanoi | Wikipedia
如果用计算机求解一个 N 圆盘的汉诺塔问题,最为简单的解决方法就是使用递归算法,思路是这样的:
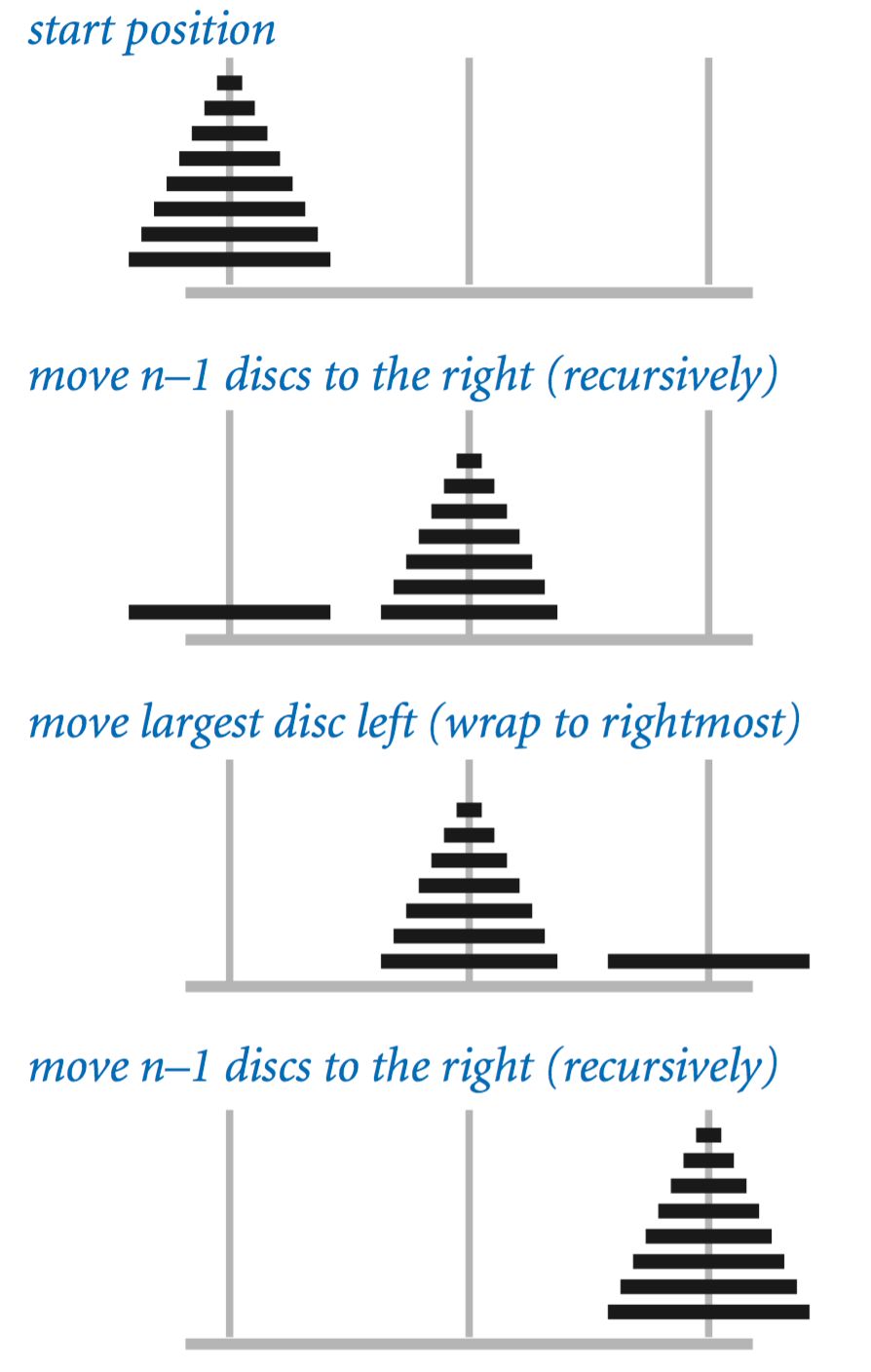
汉诺塔递归求解 | cs.princeton.edu
我们用文字描述一下:
- 先把 N - 1 个圆盘移到右边,这是一个递归
- 把最大的圆盘移到最右边
- 把 N - 1 个圆盘移到最右边,这又是个递归
在高级计算机语言里,比如 Python 或 Java 或 Go,定义好方法,几行代码就可以解决这个问题,展现了递归算法的神奇魔力。
递归树的分析
在了解了递归算法之后,我们现在使用这一思想,用 Scratch 绘制一个 递归树 Recursive Tree。
为什么递归算法可以绘制一颗树呢?我们来看一张图:
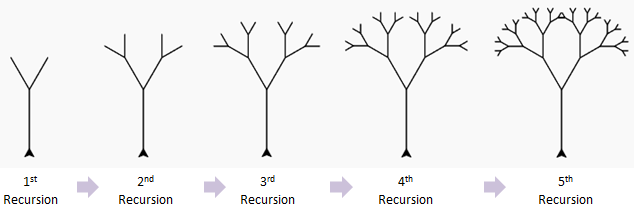
递归树分解 | 101computing
我们会发现,一颗树是由 主干 Trunk 和 分支 Branch 组成的,而每一个分支又可以看作是一颗小树的主干,于是一棵树可以这样绘制:
- 画一个主干
- 画左侧分支,当主干,绘制小树(递归)
- 画右侧分支,当主干,绘制小树(递归)
很明显,其中第二步和第三步形成了递归,因为 在方法内部调用了方法本身。
通过这样的一个过程,最终可以画出一颗大树:

一颗递归树 | Tensor-programming
思路是不是很清晰?我们开始吧~
递归树的绘制
首先,我们做一个自定义模块,绘制一颗简单的树:一个主干,左右两个分支:
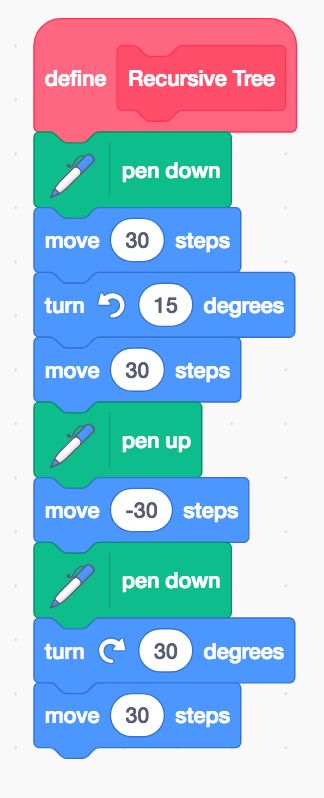
一颗简单树的模块
这棵树只有一个主干和两个分支,脚本运行时,这颗树很快就画好了:

一颗简单的树
箭头所指的就是我们上一步定义好的模块。
这时我们的绘制过程并没有使用递归算法,递归的思想在这里的体现就是在自定义模块中再次调用模块本身,于是我们对模块做了调整:
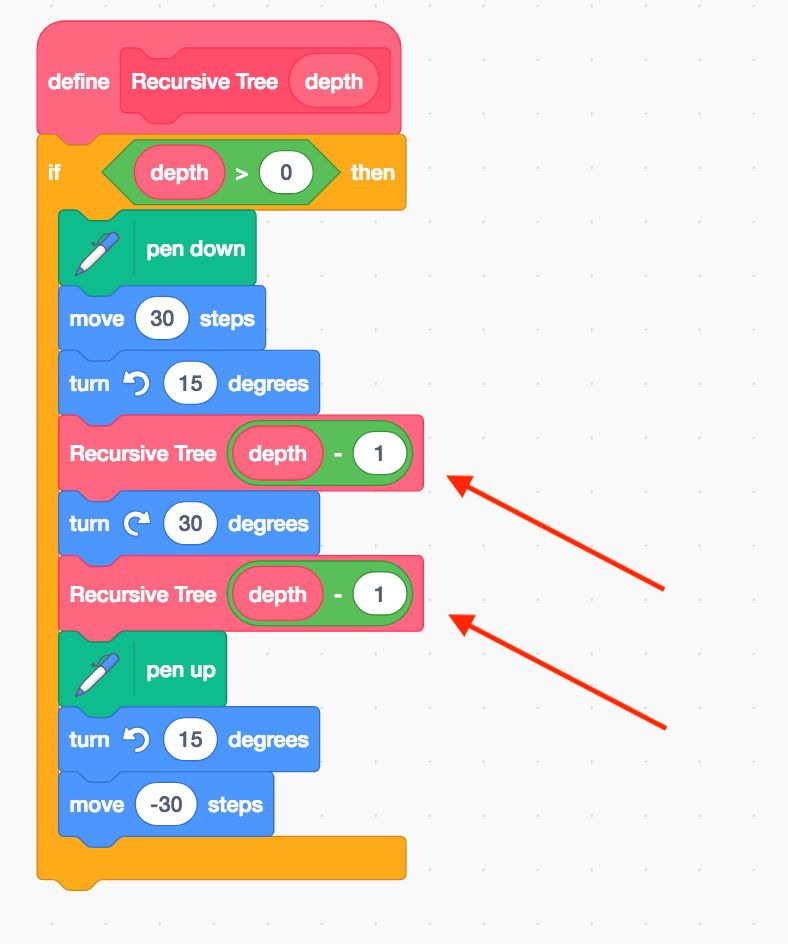
使用了递归的自定义模块
注意箭头处是两次递归调用,我们为模块添加了一个变量 depth,用这个变量表示树的 深度,运行脚本,画出来的树是这样的:
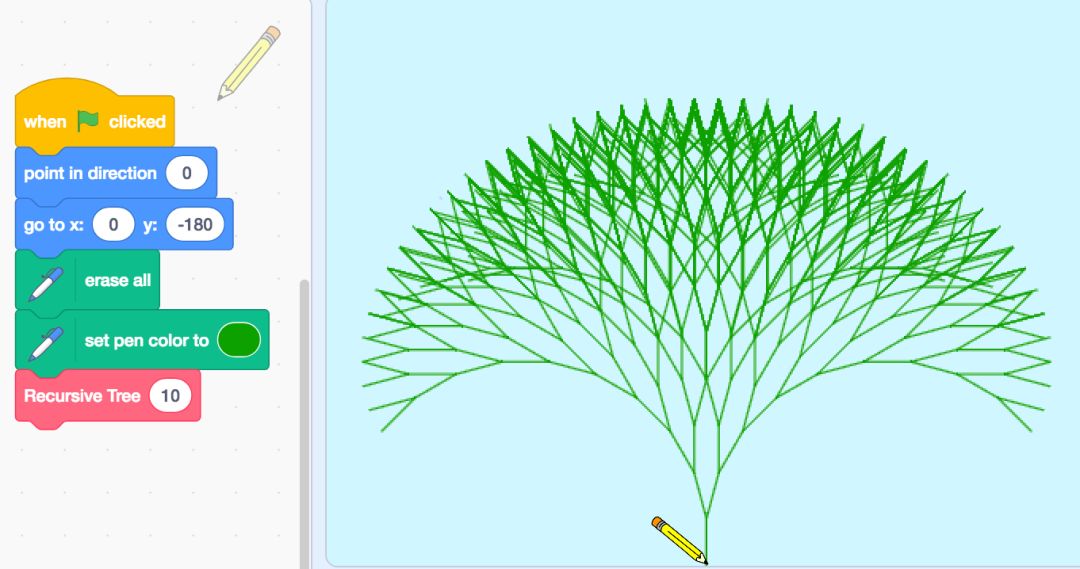
递归算法绘制的树
虽然画好了,但总感觉有些美中不足:现实中,一棵树的主干和分支长度是不一样的,粗细也是不一样的,于是我们再次调整了自定义模块:
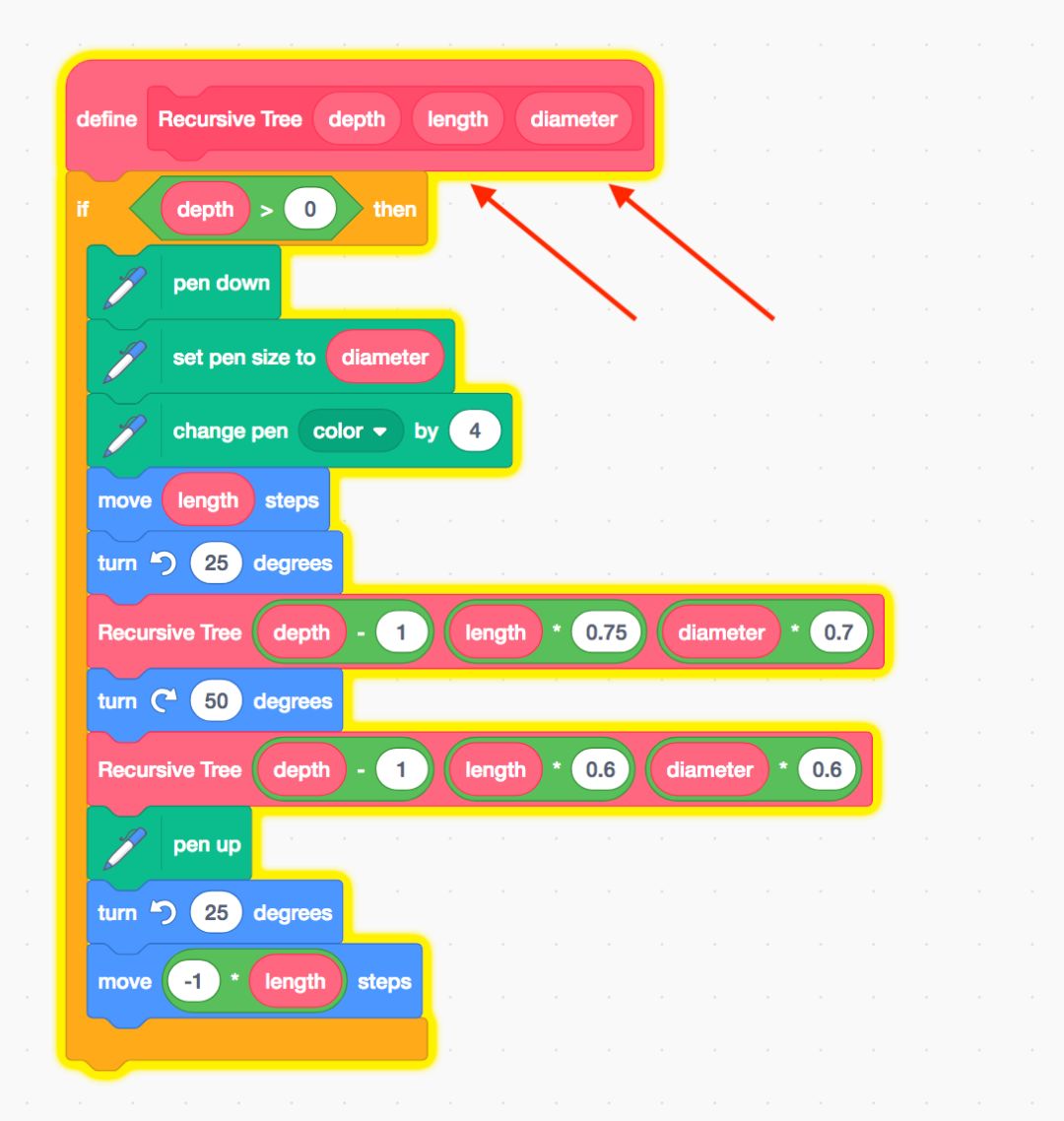
添加了两个新的变量
注意箭头处我们又添加了两个变量,length 表示树干的 长度,diameter 表示树干的 直径,每次递归过程中,我们对这两个变量都做了微调,又对树叶的颜色做了改变。
娃爸选择了一片黄土地作为背景,一颗生动的递归树就从无到有的生长出来了,贫瘠的土地焕发了生机~
最终的效果是这样的:
递归树的运行效果
今天我们还知道了以下单词的含义:
- recursion 递归
- Tower of Hanoi 汉诺塔
- tree 树
- trunk 主干
- branch 分支
- depth 深度
- length 长度
- diameter 直径
