和 Vicky 一起学习 Scratch 系列之十九 | 从星菊石到银河系

前言

上一期，我们学习了抛物线的概念和基本原理，并创作了一个月球漫步的小作品。

今天，我们学习一个有趣的数学概念 —— 斐波那契数列，不要小看这个数列，这里面可藏着自然的奥秘！

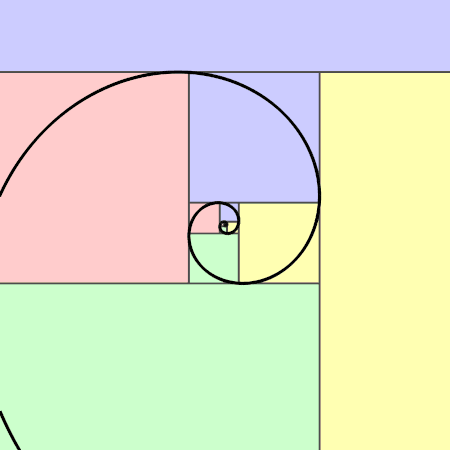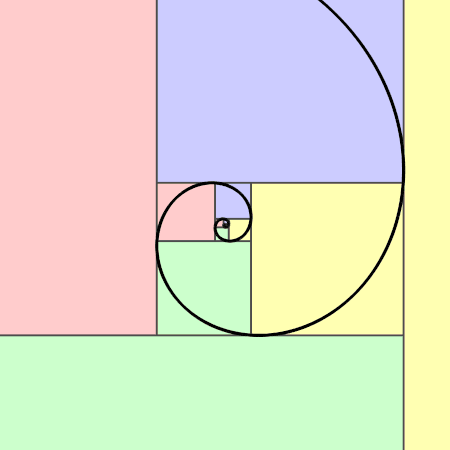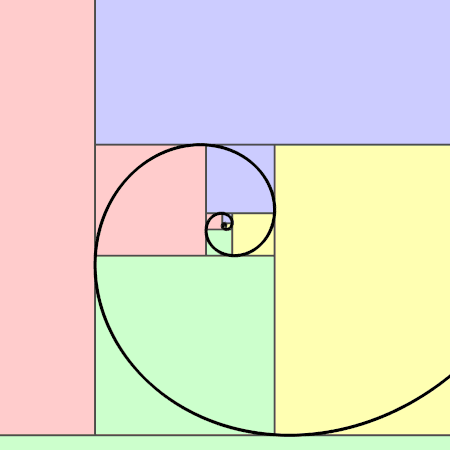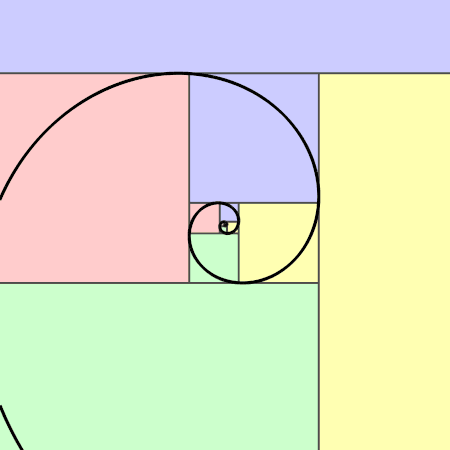
斐波那契曲线

从星菊石说起

上个周末，娃爸带着 Vicky 参观了自然博物馆，里面有各种各样的标本，从陆地到海洋，从植物到动物，令人大开眼界。

在海洋生物馆里，我们发现了一个远古时期的生物标本 —— 星菊石：

星菊石标本 | Pixnet.net

星菊石是一种生活在距今约两亿年前侏罗纪时期的海洋生物，和恐龙是同时代的物种，非常的古老。

看看它这特别的曲线，我们不禁会有这样的疑问 —— 这种曲线是怎么形成的？

其实，不光是远古时期的星菊石，现代的海洋生物也有这样的曲线：

海螺壳 | Pinterest

而且，人们又发现，不只是动物，植物也有这样的曲线：

扣形苜蓿 | Photomacrography

再到后来，人们发现，自然界中，从生物到非生物，从微观到宏观，从地球到宇宙，到处都是这样的曲线：

2018年超级台风山竹 | Wikipedia

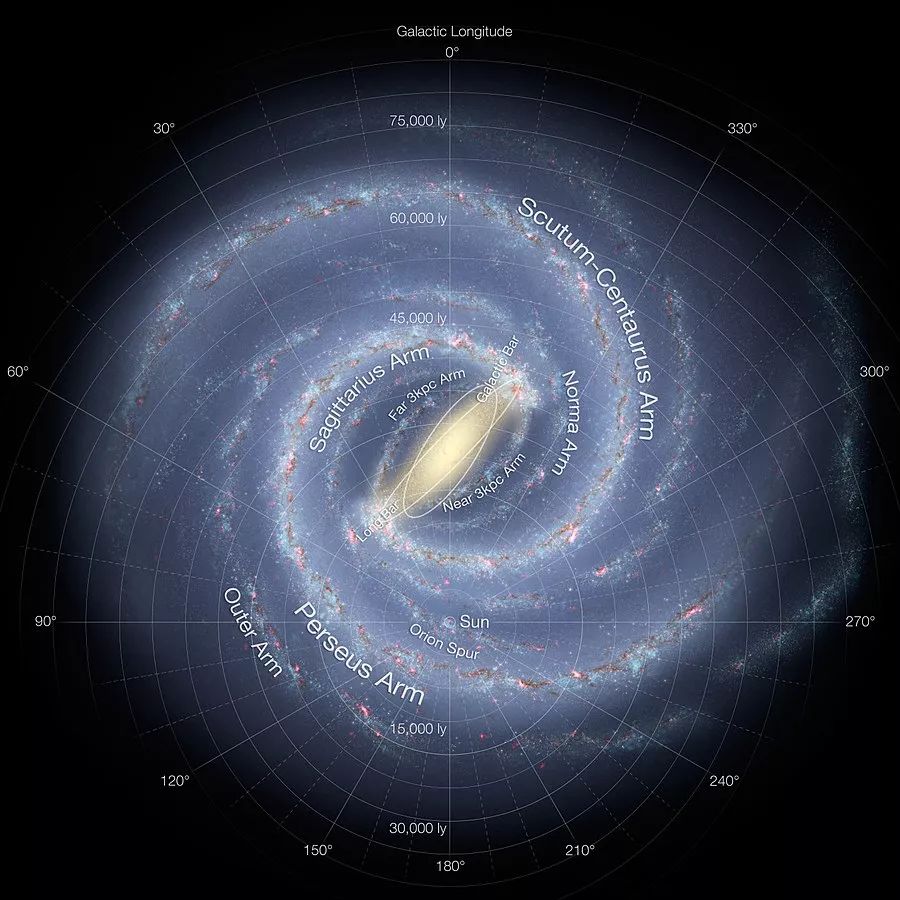
银河系旋臂 | Wikipedia

太神奇了！这里面究竟藏着怎样的奥妙玄机？

斐波那契数列

时光回转到八百年前，公元1202年，年轻的意大利数学家斐波那契在他的「计算之书」中提出一个大兔子生小兔子的问题，通过对这个问题的研究，他发现了一个新的数列，就是著名的 斐波那契数列 Fibonacci number。

这个数列的前几个数是这样的：

(0，) 1，1，2，3，5，8，13，...

Fibonacci number

聪明的你一定发现了这个数列的规律 —— 从第三个数字起，每个数字等于前面两个数字之和。

用数学公式来表达就是这样的：

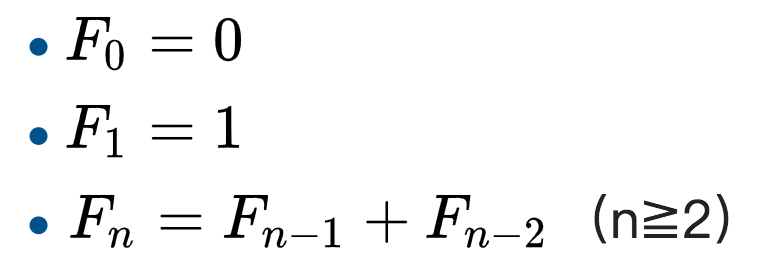
斐波那契数列公式 | Wikipedia

通过对这个数列的研究，人们画出了一条曲线，这就是著名的 斐波那契螺旋线 Fibonacci spiral，也叫做黄金螺旋曲线：

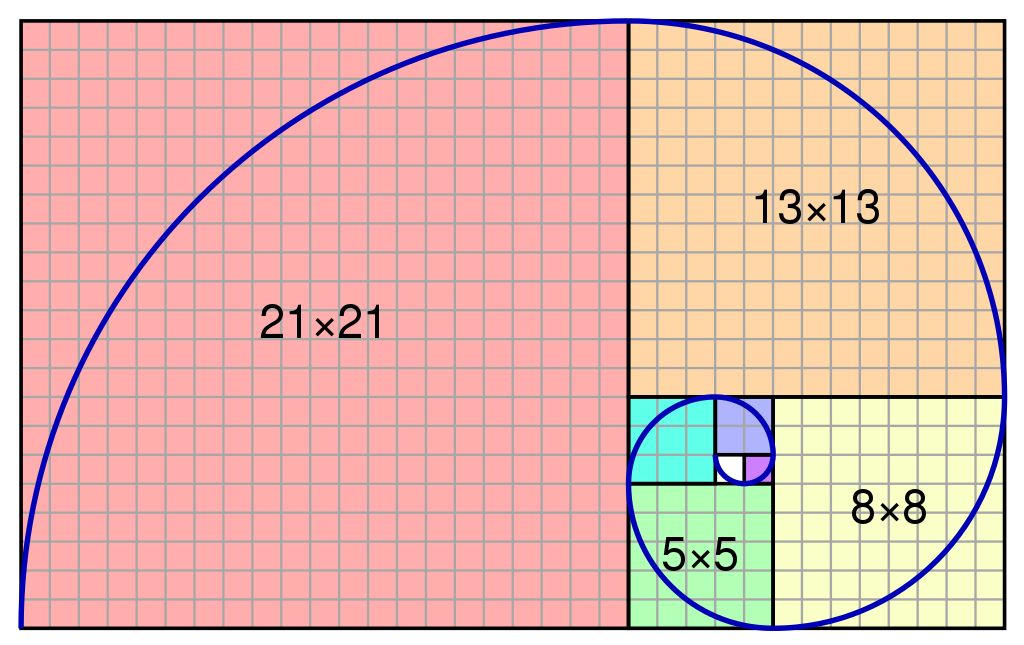
斐波那契螺旋线 | Wikipedia

而我们在上面提到的一系列事物，它们的形状和这个曲线有着高度的契合：

贝类与斐波那契螺旋线 | Ayatemplates

星系与斐波那契螺旋线 | ScienceABC

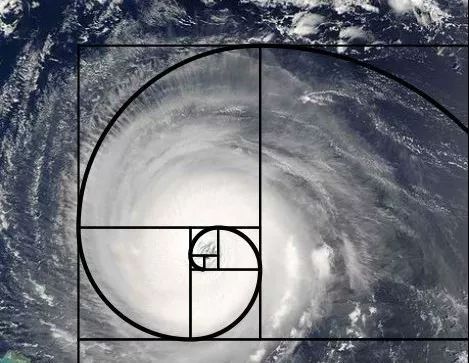
台风与斐波那契螺旋线 | Flickr

大自然中风马牛不相及的事物之间居然有这样的内在联系，让人不得不惊叹造物的神奇～

所以，有人将斐波那契螺旋线叫做 “上帝的指纹 God‘s fingerprints”，真是毫不为过。

绘制斐波那契螺旋线

在了解了斐波那契数列和螺旋线之后，我们现在用 Scratch 绘制一条斐波那契螺旋线吧～

不难发现，斐波那契螺旋线是由一系列半径不同的四分之一圆弧拼接而成：

Goden Spiral | Intmath

而这些圆弧的半径就是斐波那契数列的值：

1，1，2，3，5，8，13，21， 34，...

圆弧的半径

我们使用往期课上学过的画笔模块先来画一个半径为 100 的四分之一圆弧。

如果以坐标系的原点为圆心，这个半圆的方程是：

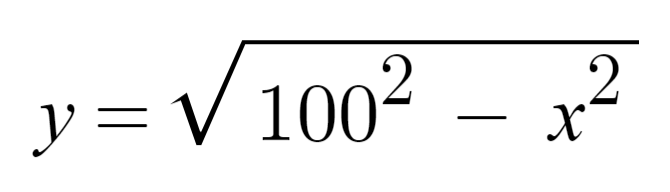
半径为 100 的半圆方程

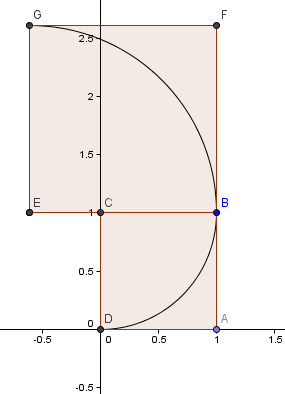
所以，我们让横坐标 x 从 0 变化到 100，求出每个点上纵坐标 y 的值，就可以画出四分之一个圆弧，脚本和效果是这样的：

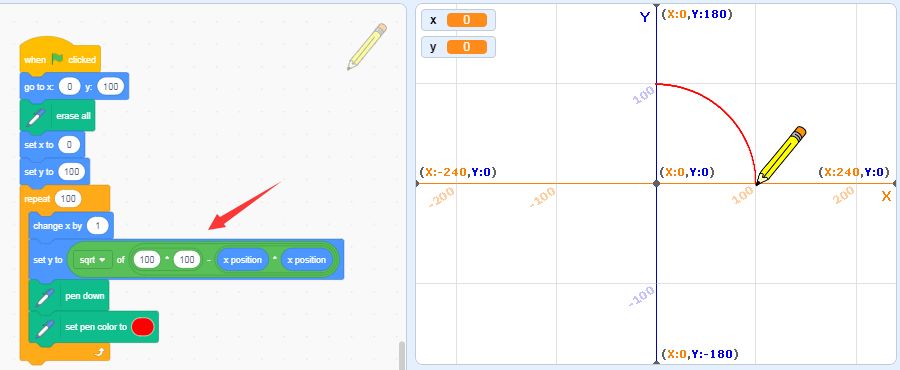
四分之一圆弧的绘制

注意箭头所指就是方程本身。好，这样我们就画好了一个圆弧，其他圆弧的绘制也是同样的方式。

为了便于圆形的绘制，我们可以声明了一个自定义模块，传入不同的参数就可以画出一个四分之一圆。

最后，娃爸画了九段互相衔接的圆弧，拼接成了一条斐波那契螺旋线，并变换了曲线的颜色。

把它放在星空的背景下，这条的神奇的曲线一直延伸到了宇宙的深处...

最终的效果是这样的：

Scratch 绘制 Fibonacci Spiral

今天我们还知道了以下单词的含义：

• fibonacci 斐波那契
• spiral 螺旋
• fingerprint 指纹

---